Path Clearance

Summary

Refractivity in the Atmosphere

Propagation in Standard Atmosphere

_______________________________________________________________

Summary

In this Session the effect of the atmosphere on radio ray trajectories is first considered, by introducing the k-factor concept; possible deviations from standard conditions are identified, as well as the minimum k-factor value. Then the Fresnel ellipsoid is defined; the partial obstruction of the ellipsoid leads to the estimate of the resultant loss. Finally, the previous concepts are used to set clearance criteria and to discuss their application to path profile analysis.

Refractivity in the Atmosphere

The Refractive Index n in a given medium is defined as the ratio of the speed of radio waves in vacuum to the speed in that medium. Since the speed of radio waves in the atmosphere is just slightly lower than in vacuum, then the Refractive Index in the atmosphere is greater than, but very close to, 1.

However, also small variations in the atmosphere Refractive Index have significant effects on radio wave propagation. For this reason, instead of using the Refractive Index n (close to 1), it is convenient to define the Refractivity N as :

So, N is the number of parts per million that the Refractive Index exceeds unity; it is a dimensionless parameter, measured in N-units.

The atmosphere Refractivity is a function of Temperature, Pressure, and Humidity. The ITU-R Rec. 453 gives the formula :

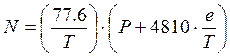
where :

T = absolute temperature (Kelvin deg);

P = atmospheric pressure (hPa, numerically equal to millibar);

e = water vapour pressure (hPa).

At sea level, the average value of N is about No = 315 N-units. The ITU-R gives world maps with the mean values of No in the months of February and August.

Temperature, atmospheric pressure, and water vapour pressure are not constant with height. This produces a Vertical Refractivity Gradient G (measured in N-units per km, N/km), defined as:

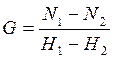
where N₁ and N₂ are the refractivity values at elevations H₁ and H₂, respectively.

Under normal (standard) atmospheric conditions, Refractivity decreases at a constant rate, moving from ground level up to about 1 km height. This means that the Refractivity Gradient G is constant, the typical value being about -40 N/km.

Deviation from the Standard Atmosphere condition is usually associated with particular weather events, like temperature inversion, very high evaporation and humidity, passage of cold air over warm surfaces or vice versa. In these conditions, the Vertical Refractivity Gradient is no longer constant. A number of different profiles have been observed and measured. It is worth noting that, at greater altitude, the Refractive Index is, in any case, closer and closer to 1; so the Refractivity N decreases to zero.

Propagation in Standard Atmosphere

A Radio Wave propagates in the direction normal to the iso-phase plane (the plane where all the points are phase synchronous, with respect to the sinusoidal pattern of electric and magnetic fields).

In a homogeneous medium, the iso-phase planes are parallel to each other and the propagation direction is a straight line normal to them.

As seen above, the Atmosphere is not a homogeneous medium and the Vertical Refractivity Gradient gives a measure of that. Different Refractivity at different heights means different propagation speeds. The wave-front moves faster or slower, depending on the height: this causes a rotation of the wave-front itself.

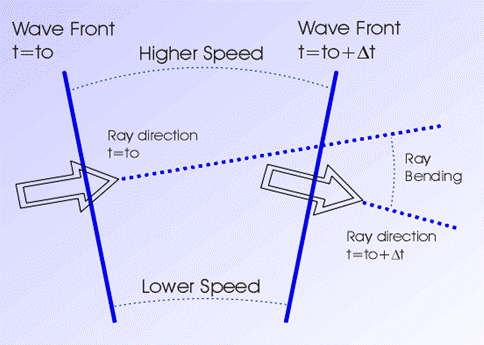
Wave Front

Wave-front and ray rotation

caused by a vertical refractivity gradient in the atmosphere

So, the propagation trajectory (normal to the wave-front) is not a straight line, but it is rotated, as shown in the above figure. Taking into account that the propagation speed is inversely proportional to the refractive index, it is possible to derive that the radio trajectory curvature 1/r is related to the Vertical Refractivity Gradient G, as :

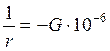
In Standard Atmosphere, with a typical value of the Refractivity Gradient G = -40 N/km, the curvature of the radio ray trajectory is :

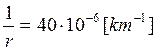
This means that the radio ray is bent downward, with a curvature 1/r, somewhat lower (less curved) than the Earth curvature 1/R :

Ray_1

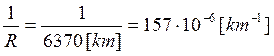
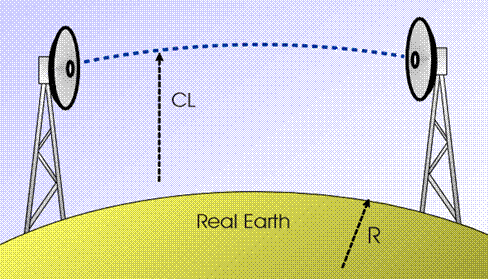
Ray bending in standard atmosphere

(CL = clearance, vertical distance from ground to ray trajectory)

The k-factor

A convenient artifice is used to account, at the same time, for both the ray and the earth curvatures. An "equivalent" representation of the above figure can be plotted by altering both curvatures by an amount equal to the ray curvature 1/r.

In the new figure (see below) the radio ray trajectory becomes a straight line, while the modified ("equivalent") earth curvature 1/R_E is :

Ray_2

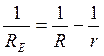
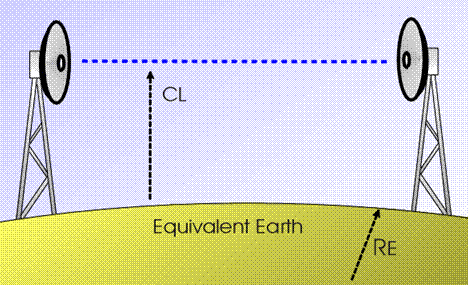
Equivalent representation of the previous figure,

with a modified earth radius R_E and a straight ray trajectory.

Note that, at any point of the radio path, the vertical distance (CL = clearance) from the earth surface to the ray trajectory is the same in the real and in the equivalent representations.

The ratio between the equivalent and the real earth radius is defined as the "effective earth-radius factor k" (briefly, the k-factor). Taking account of previous formulas, giving 1/R_E, 1/R, and 1/r , the k-factor is given by :

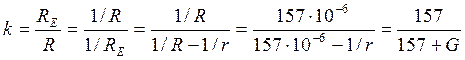
In Standard Atmosphere (G = -40 N units/km), this gives :

The k-factor gives an indication about the atmosphere state at a given time and about the bending effect on the radio ray trajectory. So, the statement "propagation at k = 4/3" is a synonymous of "propagation in Standard Atmosphere".

On the other hand, k < 4/3 corresponds to "Sub-refractive" conditions, in which the ray curvature is less than normal or even is an upward curvature ( k < 1, G > 0 ), thus reducing the clearance over ground.

With k > 4/3 we are in a "Super-refractive" atmosphere; in particular, with k = ¥, the ray trajectory is parallel to the earth surface and the signal can propagate over large distances, beyond the normal horizon.

The figure below compares the ray trajectories with different k-factors, using a "real earth" representation.

Ray_3

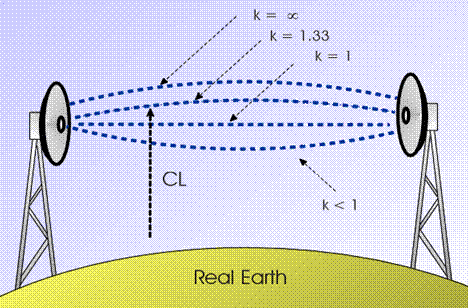
Ray bending in different atmospheric conditions

(different k-factor values)

A further alternative in plotting radio ray trajectories over the earth surface, is called "flat earth" representation

Again, both the earth and the ray curvature are altered, but in this case the earth profile is forced to be flat, while the ray curvature is modified accordingly. The "real earth" and the "flat earth" diagrams are equivalent in the sense that, at any point of the radio path, the vertical distance (CL = clearance) from the earth surface to the ray trajectory is the same in both representations.

Ray_4

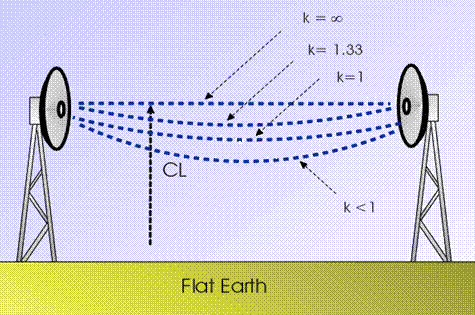
Equivalent representation of the previous figure, over flat earth

Using the "flat earth" representation, we can plot on the same diagram the path profile and multiple rays, corresponding to different values of the k-factor. This is the most usual diagram shown in computer applications for radio hop design.

k-Factor variability

We have seen that the k-factor is related to the atmosphere state and is a function of the refractivity vertical gradient. So, it is a variable parameter, depending on daily and seasonal cycles and on current meteorological conditions. In a "standard atmosphere" state the k-factor value is 4/3; this is close to the median value in most climates (particularly, temperate climates). Around this median value, the range of variations is rather wide in tropical regions, with increasing temperature and/or humidity, while it is more limited in cold and temperate climates.

Experimental observations show for example that the probability of k<0.6 in temperate climates is generally well below 1%. In tropical climates the same event is observed with probability in the range 5% - 10%. This means that, in tropical regions, there is the highest probability of propagation anomalies due to extreme k-factor values. The ITU-R gives world maps of the time percentage with G < -100 N-units / km (k > 2.75), in different months.

In discussing k-factor variability, as applied to radio hop design and to clearance criteria, we have to consider that:

· In sub-refractive conditions (minimum k-factor) the clearance over ground is reduced and the probability of obstruction is maximum.

· We are not interested in the minimum "local" k-factor, but in the overall effect through the whole radio path. So an "equivalent k-factor" (k_ea) is defined, whose minimum value depends (for given climatic conditions) on the path length. On long hops k_ea is likely to be not far from standard values, because extreme atmosphere conditions are probably not present at a time on the whole path, while in shorter hops it is more likely that particular events affect almost the whole path and produce lower k_ea values.

The ITU-R (Rec. P-530) gives a curve of minimum k_ea values as a function of hop length (temperate climate).

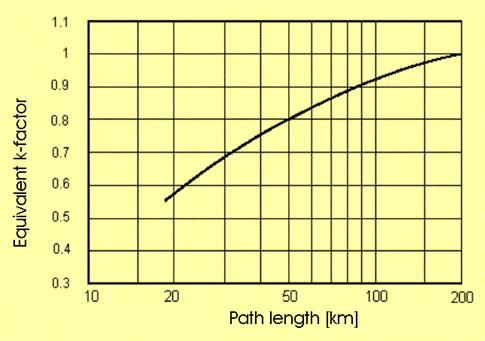
k_eff_1

Minimum equivalent k-factor vs. path length

(from ITU-R Rec. P-530, by IT permission).

Fresnel Ellipsoid

From a geometrical point of view, the Fresnel ellipsoid is defined as the set of points (P) in the space which satisfy the equation :

where Tx and Rx are the two antennas (radio path terminal points), representing the two focuses of the ellipsoid.

Ray_5

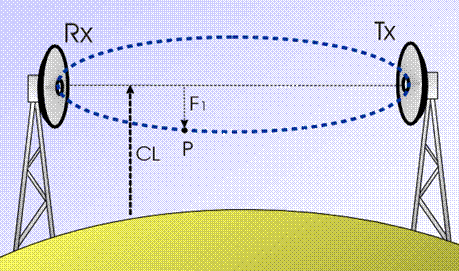
The Fresnel ellipsoid, F1 = ellipsoid radius;

CL = clearance, measured from earth surface to the ray trajectory (that is the ellipsoid longitudinal axis)

The radioelectrical interpretation of the Fresnel ellipsoid is that two rays, following the paths Tx-Rx and Tx-P-Rx, arrive at the Rx antenna in phase opposition (half-wavelength path difference, then 180 deg phase shift).

The Fresnel ellipsoid radius F1 (in meters), at a distance D1 from one of the radio sites, is given by :

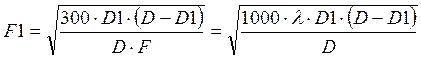
where D (km) is the path length, F (GHz) is the frequency and l (m) is the wavelength. Some examples are given in the figure below; note that the Fresnel ellipsoid radius reduces as frequency increases.

path

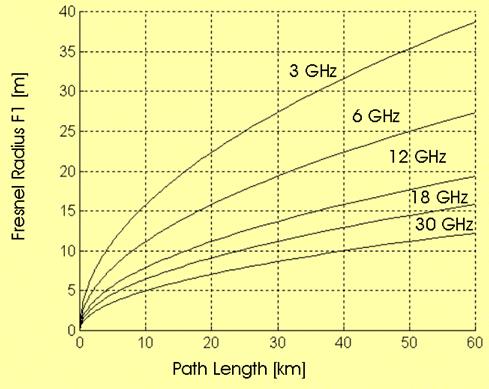
Fresnel ellipsoid radius vs. path length and frequency

(max radius, computed at mid path length).

From a practical point of view, the Fresnel ellipsoid gives a rough measure of the space volume involved in the propagation of a radiowave from a source (Tx) to a sensor (Rx). About half of the Rx signal energy travels through the Fresnel ellipsoid. So, any obstruction within the Fresnel ellipsoid has some impact on the Rx power level.

This leads to consider radio visibility in terms of clearance of the Fresnel ellipsoid, as discussed below.

A note on radio propagation and visual analogies

We are familiar with our visual experience and this can be of help in describing some aspects of radio propagation.

However, the Fresnel ellipsoid shows that radio propagation (like any EM propagation effect) cannot be explained only in terms of geometric optics, that is adequate so long as any discontinuities encountered through the propagation path are very large compared with the wavelength.

The ellipsoid radius is proportional to the wavelength square root. In our visual experience, the light wavelength is so small (about 5 10^-4 mm) that the radius of the Fresnel ellipsoid is negligible, at least as a first approximation. Diffraction effects can be observed only with accurate experiments, showing the role of Fresnel ellipsoid also in the optical field.

On the other hand, in radio communications the wavelength is in the range from 1 m (frequency 300 MHz) to about 1 cm (frequency 30 GHz), that is almost one million times larger then in visible waves.

In conclusion, much care must be paid in establishing an analogy between radio propagation and visual experience. Even if in both cases we deal with EM waves, the large difference in wavelength makes practical results quite different in most conditions. For example, the concept of Visibility is quite different in Radio Engineering and in our visual experience.

Obstruction Loss

At any point of the path profile, the Clearance (CL) is defined as the vertical distance form the ray trajectory to the ground. Since for different k-factor values a different ray trajectory is observed, then the Clearance at a given point depends on the k-factor (atmosphere state).

A negative Clearance means that an obstacle is higher than the ray trajectory (note that this is the sign convention used in ITU-R Rec. P-530, while the opposite is adopted in ITU-R Rec. P-526).

Single obstacle loss

The effect of a single obstacle, that in some measure impedes the propagation of a radio signal, is analyzed in terms of Fresnel ellipsoid obstruction. So, a Normalized Clearance is defined as C_NORM = Cl / F1, where F1 is the Fresnel ellipsoid radius.

A theoretical evaluation of diffraction loss is usually made with reference to two idealized obstacle models :

· the knife-edge obstruction, that is an obstacle with negligible thickness along the path profile;

· the smooth spherical earth, that is the obstruction produced by the earth surface for transmission beyond the horizon.

The two models represent extreme and opposite conditions and most practical cases can be assumed as intermediate between them.

The ITU-R Rec. P-530 gives obstruction loss curves (see below) for the two models mentioned above and for an intermediate case (the smooth earth result is for k = 1.33 and frequency 6.5 GHz).

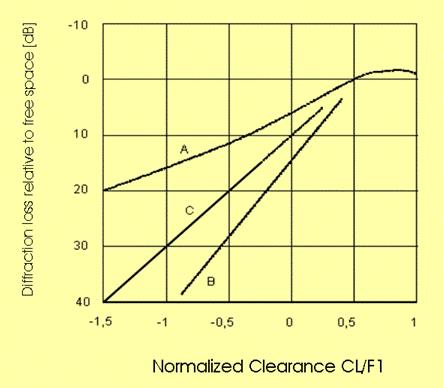
Ostruzione

Diffraction Loss vs. Normalized Clearance, with different obstacles: A) knife edge; B) smooth spherical earth; C) intermediate

(from ITU-R Rec. P-530, by ITU permission)

More on obstruction loss computation

A more detailed analysis of obstruction loss is reported in ITU-R Rec. P-526, where general formulas are given. The knife-edge model is also extended to rounded obstacles and to the case of multiple obstructions.

Knife-edge obstacle - A good approximation of the obstruction loss produced by a knife-edge obstacle is given by :

where and the approximation holds for C_NORM < 0.5.

Single rounded obstacle - The obstacle geometry is shown in the figure below, where also the relevant parameters are graphically defined.

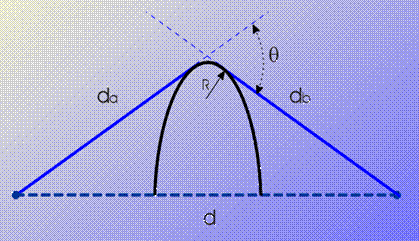
Obst1

Geometrical parameters in a rounded obstacle

(from ITU-R Rec. P-526, by ITU permission).

An approximate formula for the obstruction loss is :

where L_knife is given above and DL is the additional loss, compared with a sharp (knife-edge) obstacle, given by:

The normalized parameters n and r are computed as:

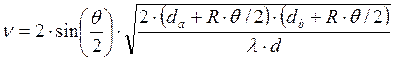
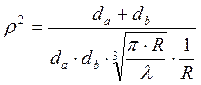
where l is the signal wavelength and the geometrical parameters (d, d_a, d_b, R, q) are defined in the figure above.

The approximation holds for :

n > 0 that is for negative clearance (obstacle above the ray trajectory);

r < 1 that, for frequency above 1 GHz, means, in practical terms, that the obstacle should not be very close to one hop terminal.

More complex formulas are proposed in the most recent version (2013) of ITU-R Rec. P.526 (sct. 4.2).

Spherical earth - At frequencies above 1 GHz, the spherical earth formulas give :

where :

and finally F is the frequency (GHz), R_E is the equivalent earth radius (8500 km for k = 1.33), D is the path length (km), H is the antenna height (m) over the earth surface; Y₁, Y₂ in the first formula refer to the first and second path terminal, respectively (in the Y formula, use the appropriate antenna height).

Multiple obstacles - Several approximate methods have been suggested to estimate the obstruction loss produced by multiple obstacles in a radio hop. It is to be noted that point-to-point links should be usually designed in such a way to avoid multiple obstacles along the radio path. However, it is useful to have computational techniques to deal also with this problem.

A reliable solution is the so-called Deygout model. Let us consider, at first, a path with two obstacles, as shown below.

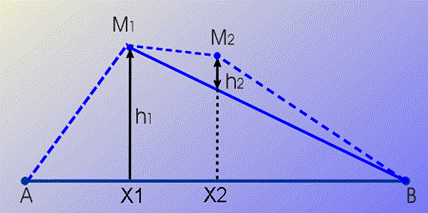
Obst2

Evaluation of two obstacle loss with the Deygout model

(from ITU-R Rec. P-526, by ITU permission).

First, the clearance is estimated at each obstacle, as if that obstacle is the only obstacle in the path. So, the "most significant obstacle" is identified, as the obstacle producing the worst (most obstructing) clearance (in the example above, this corresponds to point M1).

The overall obstruction loss L_TOTis then estimated as :

where L[XY, YZ, H] is the knife-edge obstruction loss in a radio path from X to Z, where an obstacle is at point Y with height H.

The method can be iteratively extended to more than two obstacles. For the total radio path and then for each "sub-path", the most significant obstacle is identified.

ITU-R Rec. P-526 applies the Deygout model to both knife-edge and rounded obstacles, with introduction of a correction factor (which is negligible when the obstacles are evenly spaced).

Clearance Criteria

We now have all the elements to establish Clearance Criteria in the design of a radio hop :

· the ray trajectory has been discussed and the minimum k-factor value (most critical condition) has been assessed;

· the loss produced by path obstructions has been evaluated as a function of the Normalized Clearance and using the Fresnel ellipsoid concept.

The Clearance Criteria given by ITU-R (Rec. P-530) are summarized in the figure below. They must be applied both in standard k and in minimum k conditions and take account of different climates and different obstacle shapes.

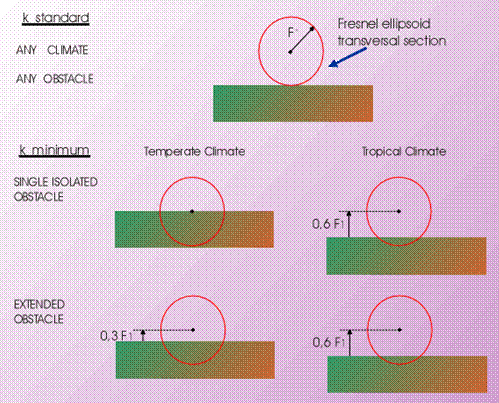
Fresnel2

A chart showing the ITU-R (Rec. P- 530) criteria for path clearance.

The red circle is the Fresnel ellipsoid transversal section,

as seen from one hop terminal, partially obstructed by the ground.

The more stringent criteria for tropical climate are justified by the wider variability in k-factor values observed in those regions.

According to ITU-R, the above rules can be made less tight, in some measure, when frequencies below 2 GHz are used. This means that smaller fractions (by about 30%) of the Fresnel radius can be adopted.

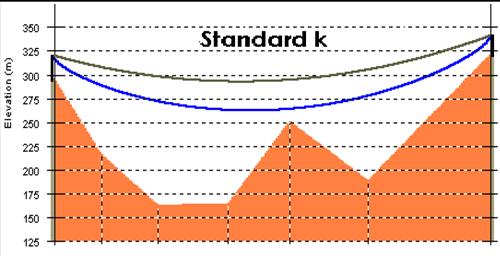
An example of application, with a single isolated obstacle, is given below, in a flat earth representation of the path profile; tropical climate is assumed. First , we check the standard-k condition (100% of the Fresnel ellipsoid free of obstacles). The two lines indicates :

· gray line: ray trajectory (ellipsoid axis) for k = 1.33;

· blue line: lower margin of the Fresnel ellipsoid (100% of the Fresnel ellipsoid radius).

Profilo_5a

Then we check the minimum-k condition (60% of the Fresnel ellipsoid free of obstacles). The three lines, in the figure below, indicates :

· gray line: ray trajectory (ellipsoid axis) for k = k min;

· red line: lower margin of the Fresnel ellipsoid (100% of the Fresnel ellipsoid radius).;

· green line: 60% of the Fresnel ellipsoid radius.

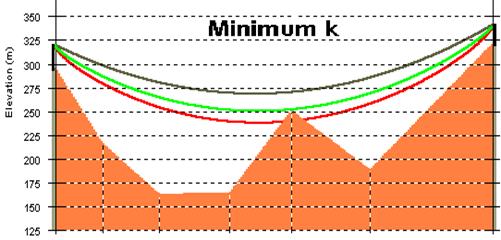
Profilo_7a

The blue and the green lines, respectively in the two diagrams, are the limiting lines to satisfy the Clearance criteria (the vertical distance from such lines to the ground is usually indicated as the "Margin").

In most cases it is sufficient to indicate those two lines (as derived for k standard and minimum values) on the profile plot and to check that none of them intercepts the path profile (positive Margin).