Rain Attenuation

Summary

EM wave interaction with atmosphere

Worldwide rain intensity statistics

ITU-R rain attenuation model

Rain unavailability prediction

HERALD Lab #6

_______________________________________________________________

Summary

In this Session we first discuss the interaction of an EM wave with molecules encountered throughout the propagation path in the atmosphere. This leads to an estimate of rain specific attenuation, as a function of rain intensity, signal frequency and polarization. Statistical data on rain intensity are considered, as required by the ITU-R rain attenuation model, which is presented as the basic tool to predict rain unavailability in any region in the world, at frequencies up to about 40 GHz.

EM wave interaction with atmosphere

Even if this Session is mainly devoted to rain effects, we first consider, in more general terms, the interaction of EM waves with molecules and particles encountered throughout the propagation path in the atmosphere.

Two effects are most significant :

· absorption: EM energy transferred to the impacted molecules and converted into heat;

· scattering: EM energy re-irradiated away from the propagation direction it had before impact.

Both effects are mainly affected by :

· Molecule / particle dimensions, relative to the wavelength of the EM radiation;

· Electrical properties of the involved molecules.

We consider the effect of the atmosphere in the absence of rain and the attenuation due to raincells.

Phenomena related to other hydrometeors (snow, ice, fog, hail) and even to dust storms will not be discussed here (ITU-R Rec. P-840 gives some indication about the effect of thick clouds and fog).

Water vapour and Oxygen attenuation in clear air

In the frequency range up to about 40 GHz, the atmospheric molecules which interacts with EM waves are water (in the form of water vapour) and, more marginally, oxygen.

A water vapour absorption peak is observed at 22.2 GHz, while the first oxygen absorption peak is at about 60 GHz. Other absorption peaks, for both water vapour and oxygen, are at higher frequencies.

The maximum attenuation due to water vapour (g_WV), at 22.2 GHz, is given by (according to ITU-R Rec. P-676) :

where r is the vapour density in g/m³, the atmospheric pressure is 1013 hPa and the temperature is 15°C.

This gives a 0.30 dB/km attenuation at the water vapour saturation level (about 12 g/m³ at 15 °C) and 0.18 dB/km at a lower vapour density of 7.5 g/m³.

On the other hand, the specific attenuation due to oxygen exceeds 1 dB/km in the frequency range 52 to 68 GHz; the maximum attenuation, at 60 GHz, is about 16 dB/km, while at 40 GHz it is below 0.1 dB/km.

For radio hops up to about 40 GHz, the conclusion is that the power loss caused by atmospheric absorption is usually not significant. In most cases it can be neglected in the Link Budget, also considering that the hop length is anyway limited by rain attenuation.

Rain attenuation

An EM wave, traveling in a given direction through a raincell, loses part of its power in that direction, as a result of absorption and scattering effects.

In the impact with a raindrop, the total power lost depends on the "drop cross section", which is given by the sum of a scattering cross section and an absorption cross section.

The drop cross section is a function of the drop radius and of the signal wavelength.

By integrating the power lost in the impact with a single raindrop to all the raindrops in a given volume (raincell), the total loss produced within that raincell can be estimated.

To do this, suitable statistical models are needed to relate the number of raindrops in a raincell and their size distribution to the rain intensity. Such models have been tuned on the basis of a large amount of experimental data, coming from different regions in the world.

As a result, the specific rain attenuation g (dB/km) can be expressed, as a function of the rain rate R (in mm/h), by the following exponential formula:

where the parameters k and a are functions of the signal wavelength and polarization.

ITU-R Rec. P-838 gives a table with the k and a values, for Vertical and Horizontal polarizations, in the frequency range 1 to 400 GHz. Formulas are given for the case of any linear or circular polarization.

Examples of specific rain attenuation as a function of rain rate, are given in the figure below; note that the increase in specific attenuation is about 100 times, when passing from 3 to 12 GHz. Moreover, the Vertical polarization is significantly less attenuated than Horizontal polarization, at the same frequency.

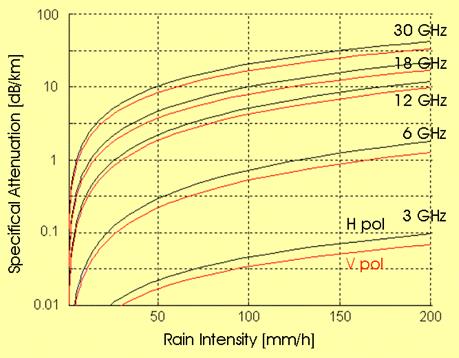
Atten

Attenuation vs. rain intensity, for different signal frequencies,

vertical (red) and horizontal (black) polarizations

Other rain impairments

EM wave depolarization - An additional effect must be considered when a linearly polarized EM wave travels through a raincell: a rotation of the polarization plane, so that an orthogonally polarized component can be observed at the output of the cell.

The de-polarization effect is related to the raindrop shape and to the dropping angle (in most cases, not perfectly vertical).

It is possible to establish a statistical relation between rain attenuation and depolarization effect. For a given probability P, we define the "equi-probable" levels in co-polar attenuation (CPA_P) and cross-polar discrimination (XPD_P) as:

XPD_P can be predicted from CPA_P (that is when the CPA cumulative distribution is known) as:

where :

Interference due to wave scattering - A raincell may become a potential source of interference to other radio systems, since part of the EM energy which impacts the cell is scattered in multiple directions. The propagation model to be applied in such conditions is described by ITU-R Rec. P.452-10.

It is rather unlikely that a P-P link may produce a significant interference effect to another P-P link, through raincell scattering. The TX power level is usually at (or below) 1 W and the cell scattering works almost like an omnidirectional radiator, so a low power density is associated with the scattered signal.

On the other hand, high power radio transmitters, in particular large earth stations for satellite communications, have the potential for producing a not negligible interference through raincell scattering. Detailed procedures are recommended by ITU-R documents to take account of this, when the satellite system operates in frequency bands shared with terrestrial systems.

Worldwide rain intensity statistics

An important input to any rain attenuation model is the expected rain activity in the region where the radio hop will operate, as derived from long-term statistics.

More specifically, it was found useful to refer to the low-probability tails of rain statistics, since we are mainly interested in rare events with very heavy rainfall.

The rain rate exceeded for 0.01% of the time is the significant parameter, useful to characterize the rainfall activity in a given region.

If possible, this rain rate should be derived from reliable statistical data about the local rain events. When local data are not available, the procedure recommended by ITU-R can be used.

In the last release of Rec. P-837 a new approach is reported to estimate the rain rate exceeded for any percentage of time, in any part of the world. This is based on data files (available from the ITU website), derived from 15 years of data of the European Centre of Medium-range Weather Forecast (ECMWF). They cover all the world, with latitude and longitude grids in 1.5° steps. A suitable interpolation procedure is recommended.

To give an approximate information about the rain rates used in rain attenuation predictions, the previous ITU-R approach is reported, which was based on world maps with "rain regions".

Each region was labeled with a letter; in the table below, each letter is associated with the corresponding rain rate (in mm/h) exceeded for 0.01% of the time :

A	8	D	19	G	30	K	42	N	95
B	12	E	22	H	32	L	60	P	145
C	15	F	28	J	35	M	63	Q	115

The world maps are shown below.

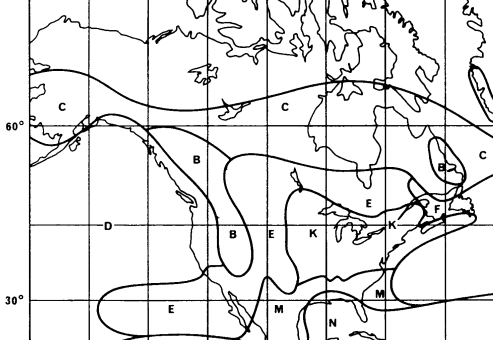
ITU-R Rain regions, North America

(from ITU-R Rec. P-837-1 Fig.1, by ITU permission)

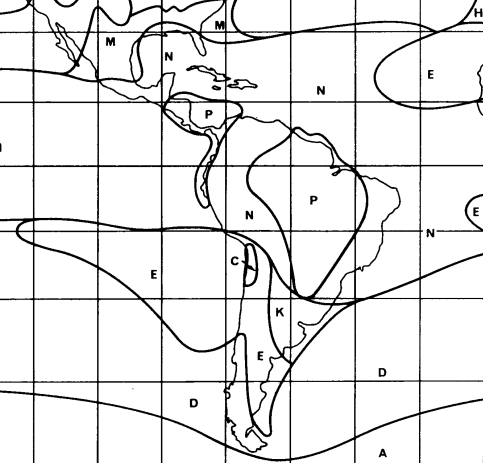
ITU-R Rain regions, Centre and South America

(from ITU-R Rec. P-837-1 Fig.1, by ITU permission)

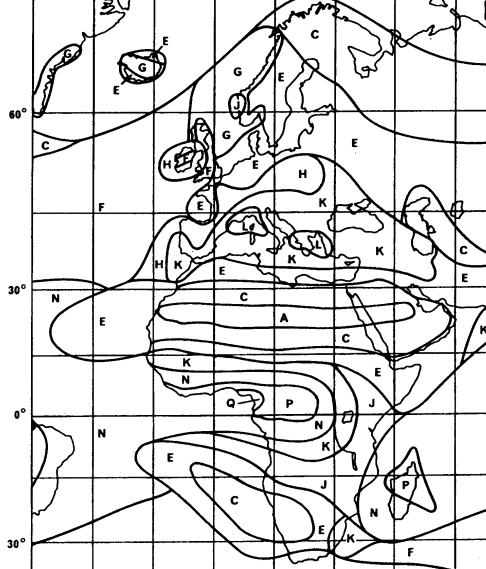
ITU-R Rain regions, Europe, Africa and Middle East

(from ITU-R Rec. P-837-1 Fig.2, by ITU permission)

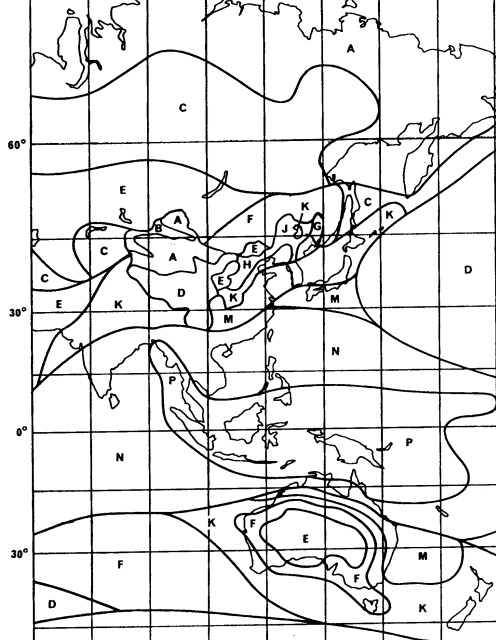
ITU-R Rain regions, Asia and Oceania

(from ITU-R Rec. P-837-1 Fig.3, by ITU permission)

ITU-R rain attenuation model

Rain intensity model

In order to apply raincell models to the estimate of rain attenuation in a radio hop, it is necessary to consider how the raincell size compare to the hop length.

While in very short hops (below some 2 - 3 km) the whole length may be affected by rainfall, in longer hops a raincell occupies only a portion of the whole distance.

ITU-R Rec. P-530 defines an "effective hop length" D_EFF, in order to take account of raincell size :

where :

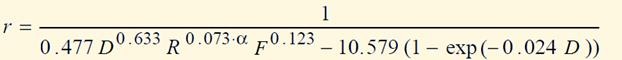
And a is theexponent of the Specific Attenuation model, previously discussed.

Note that the effective length is a function of the local rain rate R (in mm/h). As shown in the diagram below, the effective length is more compressed with high rain rates (a raincell with high rain rate is expected to occupy a smaller area). On the other hand, the effective length is close to the real length as far as the latter is approximately below 4 km.

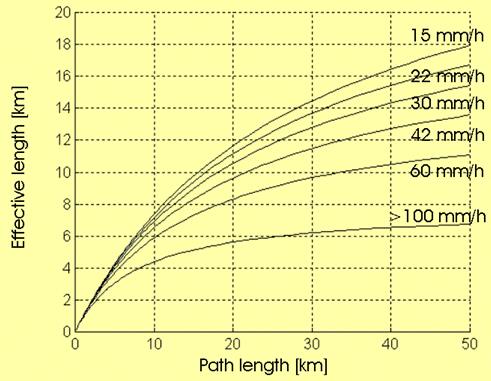
pathlen

Conversion from real path length to effective length D_EFF,

for various rain rate values

ITU-R Rec. P-530 gives a step-by-step procedure to estimate the time percentage that rain attenuation exceeds a given threshold on a radio hop.

Input parameters are the hop length, the signal frequency and polarization, and the operating region. The recommended procedure is as follows :

· Estimate of the local rain rate R for 0.01% of time. This should derive from long-term statistical data collected in the specific zone; otherwise, ITU-R data can be used, as indicated in the previous section.

· Application of the specific loss (g) formula, given the rain rate R, the signal frequency F and polarization (H or V).

· Reduction of the hop length to the Effective Length D_EFF (km), according to the above formula.

· Computation of Rain Attenuation exceeded for 0.01% of time :

· Extrapolation to other time percentages p, in the range from 1% to 0.001% :

where :

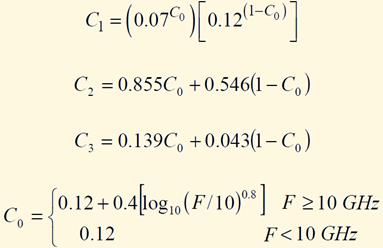
An example is given below, where A_0.01 has been assumed to be 30 dB. Note that the abscissa gives the attenuation exceeded for the corresponding time percentage.

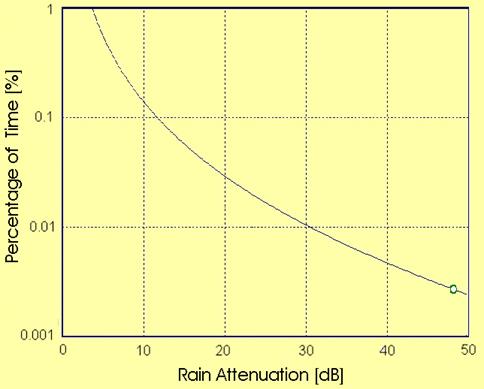
Percentage of time vs. Rain attenuation, assuming A_0.01 = 30 dB

The ITU-R prediction method is considered to be valid for frequencies up to 100 GHz and hop lengths up to 60 km.

Frequency / polarization scaling model

An alternative model proposed by ITU-R (Rec. P.530) can be applied when experimental results are available about rain attenuation on the same hop, measured at a different frequency and/or polarization.

In that case, we need to scale the measured result to the frequency and/or polarization used in the project of interest.

The following empirical formula can be used to estimate rain attenuation A₂ at frequency F₂, for a given time percentage, when long-term experimental statistics at frequency F₁ predict attenuation A₁ for the same time percentage (frequency in GHz, attenuation in dB):

where

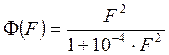
Similarly, when long-term experimental statistics on a given polarization at frequency F predict attenuation A for a given time percentage, then the attenuation on the orthogonal polarization, at the same frequency and for the same time percentage can be estimated as :

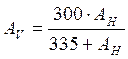
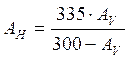
Rain unavailability prediction

For a given radio hop, the attenuation due to rain for 0.01% of the time can be estimated, according to the ITU-R procedure, as a function of the local rain rate, of the hop length, and of the signal frequency and polarization.

To predict the hop unavailability caused by rain, it is necessary to reverse the formulas given above (Attenuation vs. time percentage p), in order to get the time percentage as a function of signal attenuation (note anyway the 0.001% to 1% application range). So, rain unavailability is predicted as the probability that rain attenuation exceeds the Fade Margin FM.

The same result can be graphically derived from the Time % vs. Rain Attenuation curve.

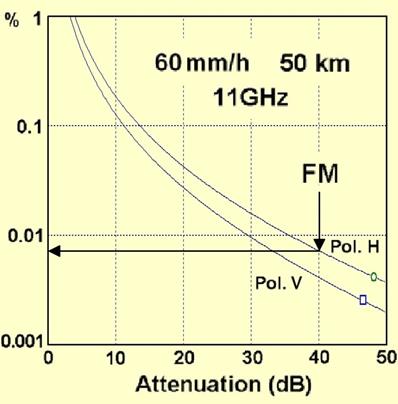
OutageRain

Rain unavailability prediction, given the hop Fade margin FM

The hop Fade Margin is computed as a result of Link Budget. In presence of heavy rainstorms, the thin water layer on the antenna radome (if used) produces an additional loss; the Fade Margin is reduced to take account of the "wet radome loss", a conservative figure being about 1 dB.

Quite often the rain unavailability prediction is transformed from a percentage probability to "minutes in one year". As a reference, the 0.01% probability is equivalent to about 50 min/year.

However, since the prediction method is based on long-term rain intensity statistics, also the estimated unavailability must be considered as an average, to be expected during a period of several years.

Effect of cross-polarized interference

Signal depolarization caused by rain contributes to rain unavailability by reducing the discrimination to a cross-polar interfering signal. Typically, the problem arises in radio systems using a co-channel frequency plan, with the same radio channel used on both polarizations.

The step-by-step procedure reported by ITU-R Rec. P.530 is as follows :

Computation of the "reference attenuation" A_P:

where U and V have been previously defined.

Computation of the normalized parameter m (if m>40, then m=40):

where A_0.01 is the attenuation exceeded for 0.01% of the time.

Estimate of probability P_XPR (unavailability due to cross-polar interference):

Reliable estimates of P_XPR are in the range 10^-2 to 10^-5.

Finally, the overall rain unavailability can be estimated as the larger of P_XPR (see above) and P_RAIN (probability of unavailability due to rain attenuation only).